дискретная экспоненциальная функция

Личные инструменты

Kapur, K.C., and Lamberson, L.R., (1977), Reliability in Engineering Design, pp 8-30, John Wiley & Sons, New York.

Как мы видим, при экспоненциальной функции распределения рисков функция плотности рисков оказывается константой (в таком случае говорят, что распределение не имеет 'памяти').

В качестве модели функции распределения рисков можно использовать различные известные функции распределения. Обычная модель - это экспоненциальное распределение рисков,

Теперь функцию интенсивности рисков можно определить следующим образом:

Функции распределения рисков соответствует некоторая функция плотности вероятности

где - время отказа.

Непрерывная Функция интенсивности рисков зависит от Функции распределения рисков , которая описывает вероятность отказа к моменту времени t:

Вычисляя дискретную функцию интенсивности рисков для всё меньших интервалов времени , мы получим ее непрерывный аналог:

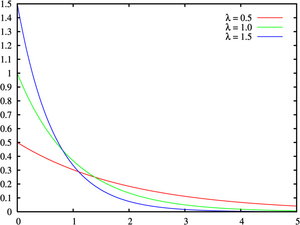
Экспоненциальные функции плотности рисков

Функция интенсивности рисков в непрерывном случае

Появление в знаменателе объясняется тем, что фактически рассматривается условная вероятность.

В дискретном случае функция интенсивности рисков понимается как того, что поломка или смерть произошла в интервале времени . Функцию плотности рисков можно определить с помощью , которая показывает вероятность отсутствия отказов до момента времени  :

Функция интенсивности в дискретном случае

Функция интенсивности рисков (этот термин был впервые использован в работе Barlow, 1963) определяется как вероятность того, что объект, выживший к началу соответствующего интервала, откажет или умрет в течение этого интервала.

Материал из MachineLearning.

Функция интенсивности рисков

Функция интенсивности рисков